Yuez
#1
在Qian的开发过程中,我们遇到了一个问题:不同的加密货币的价值显然有不同的风险,那么,如何量化不同加密货币的风险呢?
货币的对数回报率,是货币的一大重要指标,那么对数回报率的高低能不能作为货币价值风险的指标呢?在考虑这个问题之前,先问自己这么一个问题:如何定义一个货币的风险?
我们定义加密货币的风险为:在给定一个时间窗口内,货币在不发生最坏的给定概率的情况下,可能承受的最大损失比例。这个比例越大,则说明这个加密货币的风险越高。
对于我们的场景,我们关心:在1小时的时间窗口中,货币行情在不发生最坏的1%的情况下,可能承受的最大损失比例。
为了计算这个风险指数,我们使用以太坊的每小时币价数据,对其每小时的对数回报率进行研究。
一个很容易想到的问题是: 币价的涨跌有相关性吗?
相关性可能为正,也可能为负。我们的问题通俗地说就是:在相邻的两个或多个时间窗口内,涨了就更有可能接着涨吗?又或者,涨了就更有可能接着跌吗?
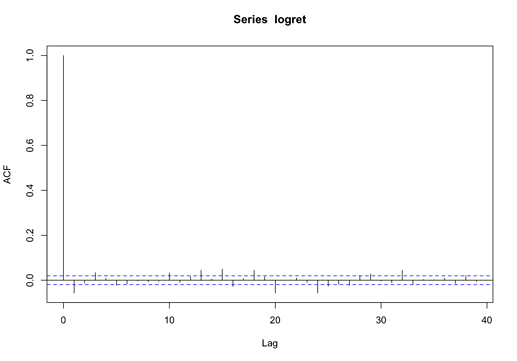
为了探究这个问题,我们对币价的对数回报率进行自相关分析,来验证币价的对数回报率的时间序列数据,是否存在自相关性,结果如下:
能够看到,币价的对数回报率的自相关性非常弱。这说明,币价在一个时间窗口之内的涨价或跌价,并不意味着在下一个时间窗口内会更有可能同向或反向发展。
Yuez
#2
继续思考,既然币价的涨跌方向难以被预估,那么我们就抛去涨跌的方向,只关心涨跌的幅度。
现实中,我们也经常有这样的情况:“啊大涨啊,好开心,我要继续投”,又过了一会儿“啊啊啊,怎么突然跌掉那么多”,再过了一会儿“咦怎么还会跌那么多”。
那么我们可以带着泪水,大胆作出如下假设:在一段大涨或大跌后,更有可能跟随着一段大涨或大跌;以此类推,在一段不活跃的行情后,也更有可能继续持续不活跃的行情。换句话说,币价的波动程度存在着聚集性,大波动往往跟随者大波动,小波动往往跟随者小波动。
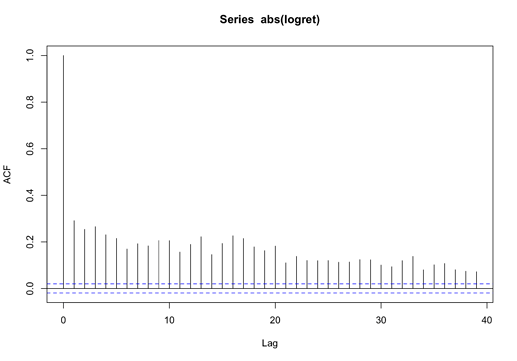
于是,我们对币价的对数回报率的绝对值进行自相关分析,来验证我们的猜测,结果如下:
我们发现了明显的自相关性,印证了我们的猜测。
这就为我们带来了一个非常符合上述特性的概率模型:广义自回归条件异方差模型。
我们将使用广义自回归条件异方差(GARCH)模型来对对数收益率的时间序列进行建模,用于解释历史数据以及估算当前时间点的资产风险。
所谓“异方差”,就是指在整个时间序列中,方差随时间变化而变化。金融数据往往呈现出波动率(即对数回报率的标准差)聚集的特性:大波动往往跟随者大波动,小波动往往跟随者小波动。因此,异方差模型相比传统计量经济学中基于方差恒定的假设的模型相比,更加能够准确地解释和模拟对数回报率的时间序列的波动率的变化,从而可以更准确地估算我们需要的风险指数。
要使用GARCH模型,我们还缺少一些信息,那就是,对数收益率本身的统计学特征。
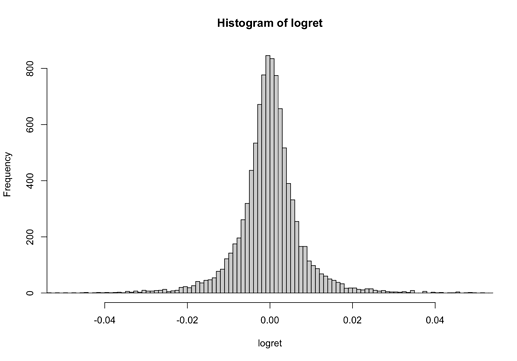
我们检验,货币的对数收益率是否符合正态分布,结果发现,货币的对数收益率的分布呈左偏和高峰度的特征,故不符合正态分布,而更加符合 Student's t 分布。
以此,我们得到了使用的 GARCH(1, 1) - Student’s t 模型,表示为:
(1) r_t = a_0 + 𝜎_t ^ 2 * 𝜀_t
(2) 𝜎_t ^ 2 = 𝛼_0 + 𝛽_1 * 𝜎_{t -1} ^ 2 + 𝛼_1 * 𝜀_{t-1} ^ 2
(3) 𝜀_t ~ t(𝜈) / sqrt(𝜈 / (𝜈 - 2))
其中:
- r_t是方差不恒定的对数回报率的时间序列
- a_0是对数回报率的数学期望,一般非常接近于零
- 𝜎_t ^ 2 * 𝜀_t 是期望外的对数回报
- 𝜎_t ^ 2是随时间变化的可预测的方差
- 𝜀_t是对数收益率的残差的时间序列,符合Student’s t分布
等式(1)表示:时间段t的对数回报率由期望中的回报率加上期望外的回报率组成。
等式(2)来自于自回归滑动平均模型:ARMA(1, 1)。就跟字面意思一样,自回归滑动平均模型实际上来自于自回归模型和滑动平均模型。其中𝛼_0为时间序列中可达到的最小的方差,𝛼_1和𝛽_1分别为一阶滑动平均模型和一阶自回归模型中的参数。滑动平均模型实际上相当于是施加在作为白噪声的𝜀_t上的有限冲激响应,而自回归模型则用于解释对数收益率的自相关性的,而对数收益率的自相关性则体现在波动率聚集上。
等式(3)表示:对数收益率的残差的时间序列,符合Student’s t分布。虽然传统计量经济学中,经常假设对数收益率的残差,包括对数收益率本身,符合正态分布,但是实际中对数收益率的分布往往呈现出偏度小于零,超值峰度大于零的现象,就像我们先前验证的一样。因此,在实践中,Student’s t分布更能准确模拟对数收益率的现实中的分布情况。